自由群

自由群是一種特殊的群，它的迷人之處在接下來會一一看到，不過在這之前要先刻畫一下自由群的樣貌。

• 一、定義
• 二、就只是符號
• 三、自由群的凱萊圖 (Cayley Graph)
• 四、群的展示 (Presentation of Groups)
• 五、自由么半群

許多群都不是阿貝爾群，但我們仍能確定它的某些元素會滿足交換率，例如：

•  $a^{-1}\cdot a = e = a \cdot a^{-1}$
•  $a^3\cdot a^2 = a^5 = a^2\cdot a^3$

可見一個元素 $a$ 與它的高次方 $a^n$ 或反元素的高次方 $a^{-m}$ 之間無可避免的會有交換率，在任何群都如此。

而自由群某種意義上可以看成是一個交換率最少的群。除非滿足以上的情況，否則 $a\cdot b \neq b \cdot a$。來看看它的定義。

一、定義

給定一個字符的集合 $S=\{a, b, c, ...\}$ ，我們都可以用以下方法構造出一個群 $F_S$，它是由字串構成的集合：

1. 規定 $a, b, c, ...$ 等字都是 $F_S$ 中的字串（只有一個字的字串）。

2. 規定單位元素 $\varepsilon$ （空字串）與符號 $a^{-1}$, $b^{-1}$, $c^{-1}$ 也都是 $F_S$ 中的字串。

3. 兩個字串 $a$ 和 $b$ 的相乘結果定為新字串 $ab$ ，也就是單純串起來。

4. 一個字串與其他字串相乘可以串成更長，如 $(ab)\cdot (c^{-1}a) = (abc^{-1}a)$ 這樣，越串越長。這些字串也在 $F_S$ 裡面。

5. 如果字串有相鄰的 $k$ 與 $k^{-1}$ 則可以消掉，如 $a^{-1}b^{-1}bbc = a^{-1}bc$，有相鄰的同樣字符也可以簡寫為次方，如 $abbba = ab^3a$。

這個 $S$ 就稱為 $F_S$ 的生成集，$S$ 的元素稱為生成元。

二、就只是符號

注意到這些 $\{a, b, c, ..., a^{-1}, b^{-1}, c^{-1}, ... , ab, ab^{-1}a, bca^{-1}b^2, a^6...\}$ 都只是字串，而不是某個群中的未知數。然而特別的地方就是：即便我們把自由群運算規則中的 $a,b,c$ 等符號用其他群的元素取代，這些替換後的「句子」仍然有意義。

例如把 $a,b,c$ 取代成 $\mathbb R_{>0}$ 乘法群中的元素 $3,2,4$，那麼前面第 5 點的字串 $$a^{-1}b^{-1}bbc = a^{-1}bc$$ 會被取代成 $$\frac{1}{3}\cdot\frac{1}{2}\cdot 2\cdot 2 \cdot 4 = \frac{1}{3} \cdot 2 \cdot 4$$ ，果然左右算式的確是相等的，但那也只是消掉一組倒數而已。或許你會覺得這個取代後的實數乘法簡直是理所當然的廢話，那是因為替換前的字串就是記載著廢話的結構，自由群就是所有關於乘法（或加法）的廢話的蒐集。

自由群 $F_S$ 利用符號在做一些「本來就會對」的乘法。

這有時稱為自由群的泛性質，這裡暫時不介紹什麼是泛性質。

不過取代的動作不能套用到不等式中。在自由群中 $ab \neq ba$是相異的字串，但是照剛剛的取代 $3\cdot 2\neq 2\cdot 3$ 就錯了。

三、自由群的凱萊圖 (Cayley Graph)

下列這張圖取自維基百科，是自由群 $F_{\{a,b\}}$ 的凱萊圖，上面每個頂點都代表 $F_{\{a,b\}}$ 中的一個字串：中心點是空字串，從中心往右邊走一個線段等於乘上 $a$，往左則是乘以 $a^{-1}$；往上是乘以 $b$，往下則是 $b^{-1}$。

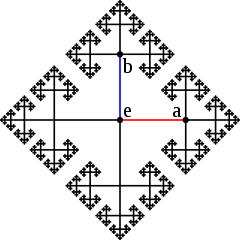
在圖中「向右再向上」與「向上再向右」會走到不同點，可見 $ab\neq ba$。由於這個圖形是無限分支下去的，因此無論多長的字串，在圖中都找得到對應點，就照著字串上的行進方向一直走就是了。。

這個圖形每個接口都是四叉路，如果換成三個生成元的自由群，圖形的每個接口就是六叉路；如果只有一個生成元，那這個自由群與無限循環群 $\mathbb Z$ 無異，圖形就是一直線。

其實這張圖可以不用畫成碎形，但是為了在畫面上擠下這麼多分枝，通常都是會畫成碎形，而且也很好看。

四、群的展示 (Presentation of Groups)

要寫出一個群，除了寫出它約定俗成的名稱（如 $\mathbb Z_2$）或寫出它的凱萊表 (Cayley Table)，還有一個常用的方式是利用群的展示 (Presentation of Groups)：列出它的所有生成元 $S$、以及生成元之間該有的關係 $R$，寫成 $\langle S|R \rangle$。

例如兩個無限循環群的直積 $\mathbb Z \otimes \mathbb Z$，寫成 $\langle a,b\ |\ ab=ba\rangle$，而有限循環群 $\mathbb{Z}_n$ 寫成 $\langle a\ |\ a^n=e\rangle$.

關於群的展示一言難盡，詳細說明可以看維基百科：群的展示。

方才說自由群 $F_S$ 是交換律最少的群，非不得已任兩個元素之間都沒有交換律（$ab$ 字串與 $ba$ 字串是不同字串），這可以看成自由群的生成元之間不存在任何關係，因此由 $S=\{a,b,c,...\}$ 生成的自由群 $F_S$ 寫起來就是 $\langle S\ |\ \varnothing\rangle$.

從凱萊圖上看起來，自由群的生成元之間不存在任何關係，代表它的凱萊圖上沒有迴路。當我們在寫其他群 $G$ 的展示，其實是準備一個由 $G$ 的生成元 $S$ 生成的自由群 $F_S$，再把 $F_S$ 的凱萊圖上的某些「樹枝」整捆整捆拗在一起。

五、自由么半群

自由么半群的部份是針對電腦科學的討論，可以忽略。

研究過計算理論或形式語言的同學可能會覺得自由群很像 regular expression 中的 * 算符（Kleene star），例如 {a,b}* 會匹配 {'',a,b,ab,ba,aba,bab,bba,bbb,aab...} 等所有字串。

與自由群不同的是，利用 Kleene star 製造不出含有 $a^{-1}$、$b^{-1}...$ 的字串，因此 Kleene star 並不會替你製造一個自由群：它製造的是「自由么半群」。所謂么半群 (Monoid) 是一種比群更弱的結構，么半群中並不要求反元素的存在。

除此之外 Kleene star 是給你一個集合，而不是代數結構，代表它製造出自由么半群之後便讓那個么半群忘掉自己的運算模式，成為一個純粹的集合。從範疇論來說就是先丟進一個自由函子成為么半群，再用遺忘函子打回集合的原形。